Symmetric Scales

Introduction

One of the things i’ve been working on during the past years is the concept of symmetry in music. So … what is symmetry when it comes to musical concepts ?

Generally speaking, we say that a musical material is symmetric when it is constructed on a division of the octave in equal parts. OK … let’s start from zero and see the meaning and implication of this statement, when it comes to scales.

A very important property of the human brain is the aptitude to identify two musical items played at different octaves as being the same thing, but in different registers. It seems so obvious to us that we never think about it, but it is actually very important for composers to be able to give some logic, construction and meaning to music.

The modern western music system is based on the division of the octave in 12 equal parts, called semitones: the smallest interval possible between 2 consecutive notes. Though, we have 12 notes at our disposal to build any musical material. A scale can then be considered as a subset of the 12 available notes. The complete set is called the chromatic scale.

A scale has two important properties: its root, which is a particular note of the scale that is used as a reference for the perception of the other notes of the scale; and its type, or quality, that defines how the other notes of the scale are related to the root. In the C major scale, C is the root, major is the quality. Nothing complicated so far …

There are 2 ways of defining a scale quality: by the intervals of each note with the root and by the succession of the intervals between each consecutive note. Using the first way, the major quality is defined by 1 2 3 4 5 6 7, representing the sequence of the intervals of each note of the scale with the root : unison, major 2nd, major 3rd, perfect 4th etc….Using the second way, the major quality can be defined by 2212221. Each number represents the number of semitones between a note and the previous one. (Both ways are useful and should be memorized).

Here the 3 basic scales used in western music in the key of C:

We will concentrate for a moment on the second way of defining a scale, which I call the relative definition. (Each note is defined relatively to the previous note, in opposite to the first way where each note is defined in relation to the root. I call it the absolute definition). We can see that for the three scales above, there is no repeating pattern inside the relative definition. We cannot extract a smaller pattern that we could repeat various times to obtain our scale.

Major scale, absolute: 1 2 3 4 5 6 7 / relative : 2212221
Harmonic minor scale, absolute: 1 2 b3 4 5 b6 7 / relative: 2122131
Melodic minor scale, absolute: 1 2 b3 4 5 6 7 / relative: 2122221

Now let’s have a look at the Diminished Whole-Half scale:

Its relative definition is : 21212121. It’s an octotonic scale (that contains 8 notes). Here we can see that the scale is made of a smaller pattern of 2 notes: 21, that is repeated 4 times. That’s why we can talk about a whole-half (or 21 in our relative definition notation) scale to define an 8-note scale, we don’t have to precise that the name of the scale is whole-half-whole-half-whole-half-whole-half, and you know why ? Because when we repeat the 21 pattern four times, we get to the octave and we « close » the scale. Therefore, this scale is based on a division of the octave in four equal parts: It’s a symmetric scale !!

Time for a little bit of math … (nothing that’s gonna hurt you, promised)

An octave is made of 12 semitones. When we look at the relative definition of a scale, the sum of all numbers should always be equal to 12. (We could imagine a system based on scales that are bigger than the octave but it’s not the topic for now).

There are 5 ways of dividing the octave in equal parts: in 12, 6, 4, 3 and 2 equal parts. When we divide the octave in 12 equal parts, the result (called the symmetric axis) is the semitone and the material built-up of semitones is the Chromatic scale, which relative definition is 111111111111. When we divide the octave in 6 equal parts, the symmetric axis is the whole tone interval (2 semitones), and the material built-up of whole tones is the Whole-Tone scale, which relative definition is 222222. Now let’s divide the octave in 4 equal parts, we get the minor third as symmetric axis (3 semitones), and the resulting material made of minor thirds is the Diminished 7th chord, which relative definition is 3333. We can see it also as a 4-note scale. Let’s continue with the division in 3 equal parts: the symmetric axis is the major third (4 semitones), and the built-up material resulting is the Augmented triad, which relative definition is 444. And to finish with, the division of the octave in 2 equal parts results in the Tritone interval (6 semitones). The built-up material would be a 2-note scale which relative definition is 66.

Here the material resulting from the division of the octave in equal parts:

I will use an enlarged concept of the word « scale » and call this material the 5 main symmetric scales. I name these scales Symmetrical 1, Symmetrical 2, Symmetrical 3, Symmetrical 4 and Symmetrical 6.

One interesting property is that any of the note in each scale can be considered being the root, without changing the resulting quality of the scale. Try to play it on a piano, from the low register to the highest, and then back down; you will notice that your ear quickly loose the sensation of where the root is, because every note is separated from her neighbors by the same interval. Do you notice that a sort of musical blur starts to appear ? This is typical from symmetry in music !!

Still there ? OK … let’s talk a bit about the concept of modes. I assume you are familiar with the modes of the major scale (Ionian, Dorian etc…). You know that the Dorian mode is the Major scale started on the second note and so on … Let’s put this in a math way: The relative definition of the major scale is 2212221. The relative definition of the Dorian mode is 2122212, right ? Do you see what happened ? We took the first number of the major scale definition and put it at the end of the sequence. In math, this is called a circular permutation. In music, a mode. No big deal.

Obvious facts:

1.When we do a circular permutation to a scale pattern, we don’t change the total number of semitones of the pattern.

2.There are as many circular permutations as the number of notes in a scale. (After doing 7 circular permutations of the major scale, the 8th permutation give you back the major scale, right ?). …. …. …. Mmm …. Mmm …. wait, wait !! Are you sure ? Nop. You are right, the second point is not always true. If you take any of our 5 main symmetric scales, you’ve noticed that their relative definition is made of the same repeating interval (the axis). As a consequence, any circular permutation of these scales is equal to the original scale. These scales have only one mode !!

These 5 main symmetric scales are not the only symmetric scales possible, by far, but any symmetric scale in music comes from them. How does this work ?Let’s take the Symmetrical 3 scale. 3 is the number of semitones in the axis (a minor third). 3 can be decomposed in a sum of integers by 2+1. It means that a scale built by an alternance of whole tones and semitones is also symmetric, and has the same symmetry axis of 3. We know this scale well, it’s the Diminished Whole-Half scale. In our language, we will call it the Symmetrical 21 scale. The 21 sequence has one circular permutation: 12. It means that the Symmetrical 21 scale has one other mode: the Symmetrical 12 scale, known as the Half-Whole Diminished or Diminished Inverted Scale. You can see that this scale has 8 notes but only 2 modes. This is going to be characteristic of the all the symmetric scales.The consequence is that you cannot transpose the scale in the 12 keys and get 12 different scales. This scale has only 3 transpositions possible: in the keys of C,C# and D. The Eb Whole-Half Diminished scale contains the same notes as the C Whole-Half Diminished. It’s the reason why the symmetric scales are also called the modes of limited transposition. (Terminology introduced by french composer Olivier Messiaen).

Now that you understood how it works, I propose to find out all the possible symmetric scales and to classify them. The more logical way is to organize them by axis. With practice, you will realize that all the scale coming from the same axis have a « color » in common, due to the fact that they are based on the same division of the octave, and they share the same transposition properties. So, let’s start !

Symmetric Scale of axis 1

OK, this one is obvious. 1 cannot be decomposed in a sum of integers, so there is only one scale of axis 1. It’s the main scale Symmetrical 1, aka the Chromatic scale. It has only one mode and one transposition.

Symmetric Scale of axis 2

This scale is based on the division of the octave in 6 whole tones (2 semitones). 12/6=2.

2 can be decomposed in a sum of integers in only one way: 1+1. But obviously, the Symmetrical 11 scale is identical to the Symmetrical 1 scale, the Chromatic scale.So the only real symmetric scale of axis 2 is the main Symmetrical 2 scale, aka the Whole-Tone scale. It has only one mode but two transpositions. It’s the first mode of Olivier Messiaen (M1).

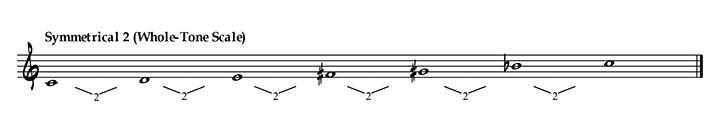
Symmetric Scales of axis 3

These scales are based on the division of the octave in 4 minor thirds (3 semitones). 12/4=3.

3 can be decomposed in a sum of integers in the following manners: 1+1+1, 2+1.

The Symmetrical 111 has again no interest, it’s the Chromatic scale. As we just saw it, the Symmetrical 21 is the Whole-Half Diminished scale, it has one circular permutation or mode: the Symmetrical 12 scale, or Half-Whole Diminished. It has 3 transpositions. It’s the second mode of Olivier Messiaen (M2).

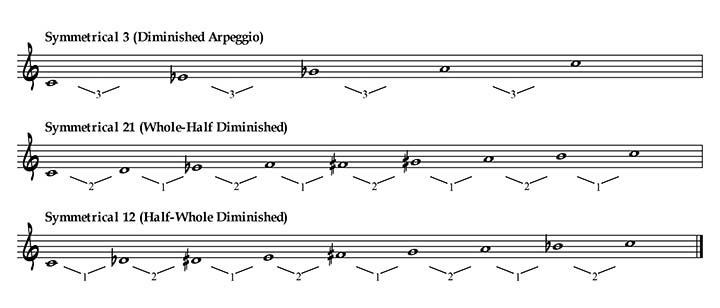
Symmetric Scales of axis 4

These scales are based on the division of the octave in 3 major thirds (4 semitones). 12/3=4.

4 can be decomposed in a sum of integers in the following manners: 1+1+1+1, 3+1, 2+2, 2+1+1.

Again, the Symmetrical 1111 has no interest. Same thing with the Symmetrical 22, which is the same as the main Symmetrical 2, the Whole-Tone scale.We are left with the Symmetrical 31 and Symmetrical 211 scales.

The Symmetrical 31 scale is known as the Symmetrical Augmented Scale. It has one circular permutation or mode: the Symmetrical 13 scale, known as Symmetrical Augmented Inverted, 6-Tone Symmetrical or Tcherepnin Hexatonic. (From Russian composer Alexander Tcherepnin).

The Symmetrical 211 is the third mode of Olivier Messiaen (M3). It has 2 circular permutations or modes: Symmetrical 112 and Symmetrical 121 (also known as Tcherepnin Enneatonic) scales.

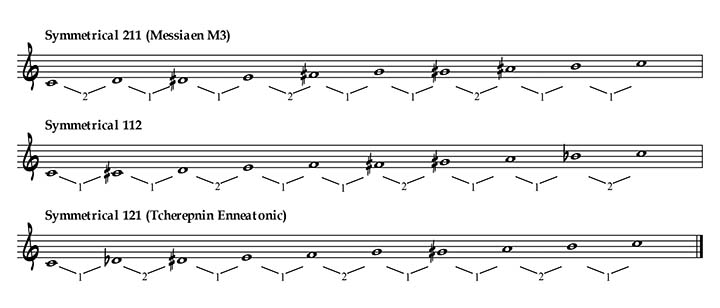
All these scales have 4 different transpositions. As you may have noticed, the number of possible transpositions is equal to the axis of the scale.

Symmetric scales of axis 6

These scales are based on the division of the octave in 2 tritones (6 semitones). 12/2=6.

Ok… things are going to get funnier.

6 can be decomposed in a sum of integers in the following manners: 5+1, 4+2, 3+3, 4+1+1, 3+2+1, 3+1+1+1, 2+2+1+1, 2+1+1+1+1+1, 1+1+1+1+1+1+1.

Symmetrical 111111 has no interest, again it’s the chromatic scale, and Symmetrical 33 is the same as the main Symmetrical 3.The Symmetrical 51 scale has one circular permutation: the Symmetrical 15 scale.

The Symmetrical 42 (a Dominant 7b5 chord) has also one circular permutation: the Symmetrical 24 scale.

The Symmetrical 411 scale has two circular permutations: the Symmetrical 114 scale (known as Two Semitones-Tritone scale), and the Symmetrical 141 scale (Fifth mode of Messiaen, M5).

Then comes the Symmetrical 321 scale. It has two circular permutations: The Symmetrical 213 and the Symmetrical 132 (known as the Tritone scale). 321 can also be arranged as 312, which is a non-circular permutation and therefore, generates a new scale that is not a mode of the Symmetrical 321: the Symmetrical 312. This new scale has also two circular permutations: The Symmetrical 123 and the Symmetrical 231 scales. It gives us a total of six scales:

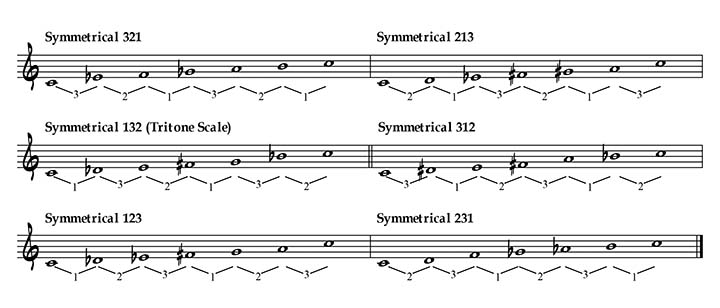
Let’s now have a look at the Symmetrical 3111 scale. It has three circular permutations: the Symmetrical 1113, 1131, 1311 scales. The Symmetrical 1131 scale is the 4th mode of Messiaen (M4).

Another octotonic scale is the Symmetrical 2211, known as the 6th mode of Messiaen (M6), with also three circular permutations: the Symmetrical 2112, 1122 and 1221 scales.

And to finish with, we have the Symmetrical 21111 scale, with four circular permutations: the Symmetrical 11112, 11121, 11211, 12111 scales. The Symmetrical 11121 scale is the 7th mode of Messiaen (M7).

And … that’s it. These are all the existing symmetric scales in the well-tempered western music system. It was not that hard finally…

Thoughts

To use these scales in an improvisational/compositional context, we need to do a melodic analysis of each scale to see on what kind of chord the scale may work. I highly recommend to do this work by yourself.

I am still in the process of learning all these scales. My personal experience is that because of their symmetric aspect, the fingering is most of the time easy to remember for the mind and body on the instrument. The drawback is that they are kind of tricky for the ear and it may really take some time to internalize the particular color of each scale.

Two remarks:

1.There are no pentatonic or heptatonic scales is this list. 5 and 7 are prime numbers, so a scale containing 5 or 7 notes cannot be splited in various equal repetitive patterns.

2. The relative high number of symmetric scales in the western music system comes from the division of the octave in 12 semitones, 12 being divisible by 2,3,4 and 6 !!! Good for us that we didn’t divided the octave in 11 or 13 parts … no symmetry would have been possible in music.What’s next ?Now, the next step is to harmonize all these scales and find out the chords we can built up out of them. I will probably dedicate a post to this topic in the future…

If this website is helping you becoming a better musician, please consider making a donation. Even a small amount will be very appreciated. Thank you !